Milenyum Problemleri, Clay Matematik Enstitüsü tarafından 2000 yılında belirlenen, hepsi de neredeyse 100 veya daha uzun yıllar önce oluşturulmuş problemlerdir. Toplamda yedi problem vardır. Bugüne kadar bunlardan sadece biri çözülebilmiştir. Problemleri çözenlere bir milyon dolar ödül verilmektedir.
Bernhard Riemann tarafından 1859 yılında ortaya atılmış bir problemdir.
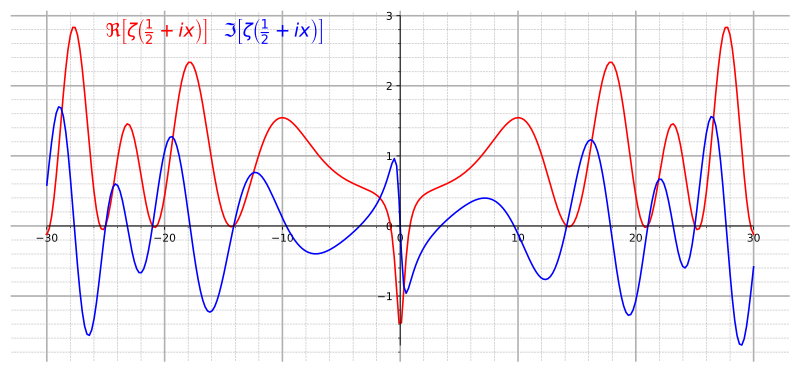
Bazı pozitif tamsayıların kendilerinden küçük ve 1'den büyük tamsayıların çarpımı (örn. 2,3,5,7,...) cinsinden yazılamayan sayılar vardır. Bu tür sayılara asal sayılar denir. Asal sayılar, hem matematik, hem de uygulama alanlarında çok önemli rol oynar. Asal sayıların tüm doğal sayılar içinde dağılımı bariz bir örüntüyü takip etmemektedir ancak Alman matematikçi Riemann, asal sayıların sıklığının; s ≠ 1 olmak koşuluyla tüm s karmaşık sayıları için;
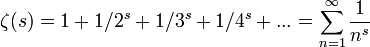
biçiminde belirtilen ve Riemann Zeta Fonksiyonu olarak bilinen fonksiyonun davranışına çok bağlı olduğunu gözlemlemiştir.
denkleminin tüm çözümleri karmaşık düzlemde bir doğru üzerinde yer almaktadır. Daha kesin bir söyleyişle, bu denklemin tüm karmaşık sayı çözümlerinin gerçel kısımlarının ½ olduğu tahmin edilmektedir. Bu iddia ilk 1.500.000.000 çözüm için sınanmıştır. Bu iddianın her çözüm için doğru olduğunun ispatlanabilmesi halinde asal sayıların dağılımı hakkında çok önemli bilgiler edinmek mümkün olacaktır.
18 Kasım 2015 tarihinde Nijeryalı Opeyemi Enoch adlı matematik profesörü, Riemann Hipotezi’ni çözdüğünü iddia etmiştir. Ancak çözümünün yanlış olduğu anlaşılmıştır.
1956 yılında ilk olarak Kurt Gödel tarafından ortaya atılmış bilgisayar bilimleri ile alakalı bir problemdir.
P harfi, polynomial (Polinom), NP harfleri ise non-deterministic polynomial (belirleyici olmayan polinom) terimlerinin kısaltmasıdır. Hesaplama teorisinde, bazı tip problemlerin çözümü için en etkili algoritmaların çalışma süresinin girilen verinin büyüklüğüne bir polinom cinsinden bağlı olduğu bilinmektedir. Buna polinomsal zamanda çalışan algoritma denir. bu tür problemler P kategorisindeki problemlerdir. Mesela verilen
basamaklı bir sayının asal olup olmadığını kontrol etmek için çalışma süresi
mertebesinde bir polinomla hesaplanabilen bir algoritma vardır. Dolayısıyla verilen bir sayının asal olup olmadığının araştırılması P kategorisinde bir problemdir.
Buna karşılık bir diğer grup problem vardır ki, bunlar için sorulan soruya girilen verinin büyüklüğüne polinom mertebesinde bağımlı bir sürede cevap verebilecek bir algoritmanın olup olmadığı bilinmemektedir. Fakat bu tür bazı problemler için eğer bir şekilde cevabı tahmin edebiliyorsak, tahminimizin doğruluğunu sınamak için veri büyüklüğüne polinom mertebesinde bağımlı sürelerde çalışacak algoritmalar vardır. Bu tür problemler, yani bir tahminin doğruluğunun kontrolü için çalışma süresi verinin büyüklüğüne polinom cinsinden bağımlı bir algoritma olan problemler de NP kategorisini oluştururlar. Örnek olarak verilen
basamaklı bir sayının asal çarpanlarının neler olduğu sorusunu düşünebiliriz. Bu sorunun cevabı için bilinen en iyi algoritmanın çalışma süresi
sayısına bir polinom cinsinden değil de eksponansiyel fonksiyonlar cinsinden (
gibi) bağımlıdır. Buna üstsel zamanda çalışan algoritma denir. Fakat bu problem için eğer bir şekilde cevabı tahmin edebiliyorsak tahminimizin doğruluğunu sınamak için
sayısına polinom mertebesinde bağımlı bir sürede çalışacak bir algoritma mevcuttur. Dolayısıyla verilen bir
basamaklı sayının asal çarpanlarının neler olduğu sorusu NP kategorisindedir.
Bu iki kategoriden NP'nin P'yi içerdiğini görmek kolaydır. Eğer bir sorunun cevabını verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalışacak bir algoritmayla bulabiliyorsak, bu soruya cevap olarak üretilmiş bir tahminin doğruluğunu da verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalışacak bir algoritmayla kontrol edebiliriz. Bunun için verilen sorunun cevabını verecek algoritmayı çalıştırıp, onun verdiği cevabı kendi tahminimizle karşılaştırmak yeterlidir. "P=NP?" problemi bunun tersinin de doğru olup olmadığını sorar. Yani problemin asıl odağı NP kategorisinde olup da P kategorisinde olmayan problemlerin varlığıdır.
Poincare Konjektürü, Henri Poincaré tarafından 1904 yılında ortaya atılmış bir teoremdir. Çözülebilen tek Milenyum Problemi'dir.
Bu teoreme göre tıkız, kenarı ve deliği olmayan üç boyutlu bir çokkatlı, yalnızca üç boyutlu bir küre olabilir.
Poincare Konjektürü, her noktası çevresinde yerel olarak üç boyutlu Öklit uzayına benzeyen topolojik uzaylara ilişkin bir önerme ifade etmektedir. Kenarsız (bir çemberin kenarı yoktur), ancak tıkız (ucu bucağı olan) böyle bir uzay düşünelim. Eğer bu uzayın içine atılmış her çember uzayın içinde kalarak bir noktaya büzülebiliyorsa (deliği yoksa), Poincare Konjektürü'ne göre bu uzay dört boyutlu Öklit uzayında yatan üç boyutlu bir küre olmalıdır. Deliği olmayan bir uzay, iki boyutlu şu basit örnekle akılda canlandırılabilir: bir elmanın kabuğuna gerilmiş paket lastiği, lastiği koparmadan ya da kabuğu parçalamadan kabuk üstündeki bir noktaya büzülebilir, ancak ortası delik bir simitte bu olanaklı değildir, delik var oldukça bazı lastikler simit yüzeyinde kalarak bir noktaya büzülemez.
Rus matematikçi Grigori Parelman, 2002 yılında bu problemin çözümünü internet üzerinden yayınlamıştır. 2006 yılında bulduğu çözümün doğruluğu kanıtlanmıştır. Parelman, problemi çözene verilecek olan bir milyon doları en başta almamış ve matematiğin Nobel'i olarak kabul edilen Fields madalyasını reddetmiştir. Problemin çözümü 492 sayfadır. Merak edenler bakabilir; http://arxiv.org/pdf/math/0607607.pdf
Şimdilik bu problemlerin net kaynakları olan 3 tanesini yazdım. Kalanları da zaman içerisinde eklerim.
1. Riemann Hipotezi
Bernhard Riemann tarafından 1859 yılında ortaya atılmış bir problemdir.
Bazı pozitif tamsayıların kendilerinden küçük ve 1'den büyük tamsayıların çarpımı (örn. 2,3,5,7,...) cinsinden yazılamayan sayılar vardır. Bu tür sayılara asal sayılar denir. Asal sayılar, hem matematik, hem de uygulama alanlarında çok önemli rol oynar. Asal sayıların tüm doğal sayılar içinde dağılımı bariz bir örüntüyü takip etmemektedir ancak Alman matematikçi Riemann, asal sayıların sıklığının; s ≠ 1 olmak koşuluyla tüm s karmaşık sayıları için;
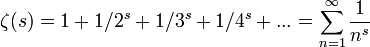
biçiminde belirtilen ve Riemann Zeta Fonksiyonu olarak bilinen fonksiyonun davranışına çok bağlı olduğunu gözlemlemiştir.
18 Kasım 2015 tarihinde Nijeryalı Opeyemi Enoch adlı matematik profesörü, Riemann Hipotezi’ni çözdüğünü iddia etmiştir. Ancak çözümünün yanlış olduğu anlaşılmıştır.
2. P=NP
1956 yılında ilk olarak Kurt Gödel tarafından ortaya atılmış bilgisayar bilimleri ile alakalı bir problemdir.
P harfi, polynomial (Polinom), NP harfleri ise non-deterministic polynomial (belirleyici olmayan polinom) terimlerinin kısaltmasıdır. Hesaplama teorisinde, bazı tip problemlerin çözümü için en etkili algoritmaların çalışma süresinin girilen verinin büyüklüğüne bir polinom cinsinden bağlı olduğu bilinmektedir. Buna polinomsal zamanda çalışan algoritma denir. bu tür problemler P kategorisindeki problemlerdir. Mesela verilen
Buna karşılık bir diğer grup problem vardır ki, bunlar için sorulan soruya girilen verinin büyüklüğüne polinom mertebesinde bağımlı bir sürede cevap verebilecek bir algoritmanın olup olmadığı bilinmemektedir. Fakat bu tür bazı problemler için eğer bir şekilde cevabı tahmin edebiliyorsak, tahminimizin doğruluğunu sınamak için veri büyüklüğüne polinom mertebesinde bağımlı sürelerde çalışacak algoritmalar vardır. Bu tür problemler, yani bir tahminin doğruluğunun kontrolü için çalışma süresi verinin büyüklüğüne polinom cinsinden bağımlı bir algoritma olan problemler de NP kategorisini oluştururlar. Örnek olarak verilen
Bu iki kategoriden NP'nin P'yi içerdiğini görmek kolaydır. Eğer bir sorunun cevabını verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalışacak bir algoritmayla bulabiliyorsak, bu soruya cevap olarak üretilmiş bir tahminin doğruluğunu da verinin büyüklüğüne polinom mertebesinde bağımlı sürede çalışacak bir algoritmayla kontrol edebiliriz. Bunun için verilen sorunun cevabını verecek algoritmayı çalıştırıp, onun verdiği cevabı kendi tahminimizle karşılaştırmak yeterlidir. "P=NP?" problemi bunun tersinin de doğru olup olmadığını sorar. Yani problemin asıl odağı NP kategorisinde olup da P kategorisinde olmayan problemlerin varlığıdır.
3. Poincare Konjektürü
Poincare Konjektürü, Henri Poincaré tarafından 1904 yılında ortaya atılmış bir teoremdir. Çözülebilen tek Milenyum Problemi'dir.
Bu teoreme göre tıkız, kenarı ve deliği olmayan üç boyutlu bir çokkatlı, yalnızca üç boyutlu bir küre olabilir.
Poincare Konjektürü, her noktası çevresinde yerel olarak üç boyutlu Öklit uzayına benzeyen topolojik uzaylara ilişkin bir önerme ifade etmektedir. Kenarsız (bir çemberin kenarı yoktur), ancak tıkız (ucu bucağı olan) böyle bir uzay düşünelim. Eğer bu uzayın içine atılmış her çember uzayın içinde kalarak bir noktaya büzülebiliyorsa (deliği yoksa), Poincare Konjektürü'ne göre bu uzay dört boyutlu Öklit uzayında yatan üç boyutlu bir küre olmalıdır. Deliği olmayan bir uzay, iki boyutlu şu basit örnekle akılda canlandırılabilir: bir elmanın kabuğuna gerilmiş paket lastiği, lastiği koparmadan ya da kabuğu parçalamadan kabuk üstündeki bir noktaya büzülebilir, ancak ortası delik bir simitte bu olanaklı değildir, delik var oldukça bazı lastikler simit yüzeyinde kalarak bir noktaya büzülemez.
Rus matematikçi Grigori Parelman, 2002 yılında bu problemin çözümünü internet üzerinden yayınlamıştır. 2006 yılında bulduğu çözümün doğruluğu kanıtlanmıştır. Parelman, problemi çözene verilecek olan bir milyon doları en başta almamış ve matematiğin Nobel'i olarak kabul edilen Fields madalyasını reddetmiştir. Problemin çözümü 492 sayfadır. Merak edenler bakabilir; http://arxiv.org/pdf/math/0607607.pdf
Şimdilik bu problemlerin net kaynakları olan 3 tanesini yazdım. Kalanları da zaman içerisinde eklerim.
Moderatör tarafında düzenlendi:
